Maths Class X
If sin (A + 2B) = √3/2 and cos (A + 4B) = 0, A > B
If sin (A + 2B) = √3/2 and cos (A + 4B) = 0, A > B, and A + 4B ≤ 90º, then find A and B.
Read more …The following frequency distribution shows the distance thrown by 68 students
The following frequency distribution shows the distance (in metres) thrown by 68 students in a Javelin throw competition.

Draw a less than type Ogive for the given data and find the median distance thrown using this curve.
Read more …The following distribution shows the daily pocket allowance of children of a locality
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs.18. Find the missing frequency k.

By changing the following frequency distribution ‘to less than type’
By changing the following frequency distribution ‘to less than type’ distribution, draw its ogive.

Find the value(s) of k for which the pair of linear equations kx + y = k^2 and x + ky = 1
Find the value(s) of k for which the pair of linear equations kx + y = k2 and x + ky = 1 have infinitely many solutions.
Read more …For what values of m and n the following system of linear equations
For what values of m and n the following system of linear equations has infinitely many solutions.
3x + 4y = 12
(m + n)x + 2(m – n)y = 5m – 1
Find all the zeroes of the polynomial 3x^4 + 6x^3 - 2x^2 - 10x - 5
Find all the zeroes of the polynomial 3x4 + 6x3 - 2x2 - 10x - 5 if two of its zeroes are √(5/3) and – √(5/3)
Read more …Obtain all zeroes of 3x^4 – 15x^3 + 13x^2 + 25x – 30
Obtain all zeroes of 3x4 – 15x3 + 13x2 + 25x – 30, if two of its zeroes are √5/3 and – √5/3
Read more …A train travelling at a uniform speed for 360 km would have taken 48 minutes less
A train travelling at a uniform speed for 360 km would have taken 48 minutes less to travel the same distance if its speed were 5 km/hour more. Find the original speed of the train.
Read more …Check whether the equation 5x^2 – 6x – 2 = 0 has real roots
Check whether the equation 5x2 – 6x – 2 = 0 has real roots and if it has, find them by the method of completing the square. Also verify that roots obtained satisfy the given equation.
Read more …A faster train takes one hour less than a slower train for a journey of 200 km
A faster train takes one hour less than a slower train for a journey of 200 km. If the speed of slower train is 10 km/hr less than that of faster train, find the speeds of two trains.
Read more …Prove that the ratio of the areas of two similar triangles is equal to
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Read more …Two poles of equal heights are standing opposite to each other
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point in between them on the road, the angles of elevation of the top of poles are 60º and 30º respectively. Find the height of the poles and the distances of the point from the poles.
Read more …If sin θ + cos θ = √2, then evaluate: tan θ + cot θ
If sin θ + cos θ = √2, then evaluate: tan θ + cot θ
Read more …The angle of elevation of the top of a hill at the foot of a tower is 60º
The angle of elevation of the top of a hill at the foot of a tower is 60º and the angle of depression from the top of tower to the foot of hill is 30º. If tower is 50 metre high, find the height of the hill.
Read more …A cone of maximum size is carved out from a cube of edge 14 cm
A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the remaining solid after the cone is carved out.
Read more …A man donates 10 aluminum buckets to an orphanage. A bucket made of aluminum is of height 20 cm
A man donates 10 aluminum buckets to an orphanage. A bucket made of aluminum is of height 20 cm and has its upper and lowest ends of radius 36 cm and 21 cm respectively. Find the cost of preparing 10 buckets if the cost of aluminum sheet is Rs. 42 per 100 cm2.
Read more …Find the mean and mode for the following data
Find the mean and mode for the following data:

A box contains cards numbered from 1 to 20. A card is drawn at random
A box contains cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that number on the drawn card is
- a prime number
- a composite number
- a number divisible by 3
A box contains cards numbered 11 to 123. A card is drawn at random from the box
A box contains cards numbered 11 to 123. A card is drawn at random from the box. Find the probability that the number on the drawn card is
- a square number
- a multiple of 7
A box contains 12 balls of which some are red in colour
A box contains 12 balls of which some are red in colour. If 6 more red balls are put in the box and a ball is drawn at random, the probability of drawing a red ball doubles than what it was before. Find the number of red balls in the bag.
Read more …The King, Queen and Jack of clubs are removed from a pack of 52 cards
The King, Queen and Jack of clubs are removed from a pack of 52 cards and then the remaining cards are well shuffled. A card is selected from the remaining cards. Find the probability of getting a card
- of spade
- of black king
- of club
- of jacks
In Figure, ABCD is a rectangle. Find the values of x and y
In Figure, ABCD is a rectangle. Find the values of x and y.

Find the ratio in which P(4, m) divides the line segment
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
Read more …Two different dice are tossed together. Find the probability of getting a doublet
Two different dice are tossed together. Find the probability:
- of getting a doublet
- of getting a sum 10, of the numbers on the two dice
An integer is chosen at random between 1 and 100
An integer is chosen at random between 1 and 100. Find the probability that it is:
- divisible by 8
- not divisible by 8
Find all zeroes of the polynomial (2x^4 – 9x^3 + 5x^2 + 3^x – 1)
Find all zeroes of the polynomial (2x4 – 9x3 + 5x2 + 3x – 1) if two of its zeroes are (2 + √3) and (2 – √3).
Read more …If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Read more …If A(–2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD
If A(–2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the lengths of its sides.
Read more …A plane left 30 minutes late than its scheduled time
A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
Read more …Prove that the area of an equilateral triangle described on one side of the square
Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.
Read more …Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region.

If the area of two similar triangles are equal, prove that they are congruent
If the area of two similar triangles are equal, prove that they are congruent.
Read more …If tan 2A = cot (A - 18°), where 2A is an acute angle
If tan 2A = cot (A - 18°), where 2A is an acute angle, find the value of A.
Read more …Find the area of the shaded region, where arcs drawn with centres A, B, C and D intersect
Find the area of the shaded region in Figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π = 3.14]

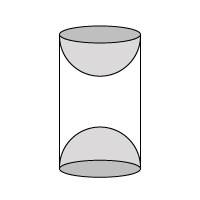
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm. Find the total surface area of the article.
A heap of rice is in the form of a cone of base diameter 24 m
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
Read more …The table below shows the salaries of 280 persons
The table below shows the salaries of 280 persons:
| Salary (In thousand Rs.) | No. of persons |
| 5-10 | 49 |
| 10-15 | 133 |
| 15-20 | 63 |
| 20-25 | 15 |
| 25-30 | 6 |
| 30-35 | 7 |
| 35-40 | 4 |
| 40-45 | 2 |
| 45-50 | 1 |
Calculate the median salary of the data.
Read more …A train travels at a certain average speed for a distance of 63 km
A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed?
Read more …A motor boat whose speed is 18 km/hr in still water takes 1 hr more to go 24 km upstream
A motor boat whose speed is 18 km/hr in still water takes 1 hr more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Read more …The sum of four consecutive numbers in an AP is 32 and the ratio of the product
The sum of four consecutive numbers in an AP is 32 and the ratio of the product of the first and the last term to the product of two middle terms is 7 : 15. Find the numbers.
Read more …The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
- The area of the metal sheet used to make the bucket.
- Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
As observed from the top of a 100 m high light house from the sea-level, the angles of depression of two ships
As observed from the top of a 100 m high light house from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships. [Use √3 = 1.732]
Read more …The mean of the following distribution is 18. Find the frequency f of the class 19 - 21
The mean of the following distribution is 18. Find the frequency f of the class 19 - 21.
| Class | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| Frequency | 3 | 6 | 9 | 13 | f | 5 | 4 |
The following distribution gives the daily income of 50 workers of a factory
The following distribution gives the daily income of 50 workers of a factory.
| Daily income (in Rs.) | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Read more …A bag contains 15 white and some black balls
A bag contains 15 white and some black balls. If the probability of drawing a black ball from the bag is thrice that of drawing a white ball, find the number of black balls in the bag.
Read more …In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm
In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. [Use π = 22/7]

Page 2 of 3
